※2025年11月20日:「簡易変換ツール」追加

プログラミングを勉強するということは「概念」を勉強することだと心得えています。
概念を勉強するということは、いかに脳内で、あるいは実際に手を動かして、現実のものと結びつけるかが重要と身に染みて感じている今日この頃です。
さて、先日「すべてがFになる」(←アマプラリンクです)というアニメをイッキ見しました。
この話は1998年に出版された小説をベースにしたアニメですが、著者の森 博嗣さんは国立大学の助教授でありながらこの小説で衝撃デビューした異色の作家さんのようです。私はこの小説の存在を知ってはいたものの、なんとなく難しそうな内容だなぁと敬遠していましたが、妻にこのアニメを紹介されたので見始めたところ面白すぎて11話分を1日で視聴してしまいました。
ご想像のとおり、この物語の鍵を握るのがタイトルにもなっている「すべてがFになる」というキーワードです。
知らない方にはちょっとネタバレになってしまいますが、この「F」は16進数のことであり、これが物語の謎を紐解く重要な鍵になっています。興味がある方は実際にご覧になってみてください。とても面白いですよ。
というわけで、何にでもすぐに感化されてしまう癖を持つ私は、アニメを見るだけで飽き足らず、応用情報技術者試験の教科書でこの16進数を調べはじめたわけですが、せっかくなので、最初の基礎理論で学ぶことになる「○〇進数」(主に2進数)について私のようなリスキリング目的の方のために私なりの理解を記事にまとめておこうと思います。
16進数について
物語では16進数において1桁目の最後を数を表す「F」が謎解きの重要なキーワードとなり、度々登場するのですが、実際のコンピュータの世界でも、この16進数は文字や色を表したり、メモリのアドレスなどに使われていたり、様々な使われ方をしています。
16進数で表したサンプル※
※このサンプルはAI(Gemini Advanced)による生成です
色コード
- #FF0000: 赤色 (Red)
- #00FF00: 緑色 (Green)
- #0000FF: 青色 (Blue)
- #FFFF00: 黄色 (Yellow)
- #808080: 灰色 (Gray)
Webページのスタイルシート (CSS) や画像編集ソフトなどで、上記のような16進数で色を指定できます。最初の2桁が赤(R)、次の2桁が緑(G)、最後の2桁が青(B)の成分を表し、それぞれ00 (なし) から FF (最大) までの値を取ります。
メモリアドレス
- 0x0000: メモリの先頭アドレス
- 0x7FFF: 16ビットCPUでアクセス可能な最大のアドレス
- 0x10000: 64KB境界
- 0x100000: 1MB境界
メモリアドレスは、コンピュータのメモリ上の特定の場所を示すために使用されます。16進数で表現されることが一般的で、”0x”というプレフィックスが付くことが多いです。
文字コード (Unicode)
- 0x0041: ラテン大文字 A (Latin capital letter A)
- 0x0061: ラテン小文字 a (Latin small letter a)
- 0x3042: ひらがな あ (Hiragana letter A)
- 0x4E00: 漢字 一 (CJK unified ideograph-4E00)
- 0x1F600: 😀 (grinning face)
Unicodeは、世界中の文字を統一的に扱うための文字コード体系です。各文字に16進数のコードポイントが割り当てられています。
〇〇進数対応表
16進数は、このように様々な使われ方をするのですが、なぜ16進数が使われるかというと、それはたぶん2進数と相性が良いからです。
16進数における1桁(0~F(10進数における0~15))が2進数における4桁(0000~1111)にぴったり対応します。
以下のように対応しています。
| 10進数 | 2進数 | 16進数 |
|---|---|---|
| 1 | 0001 | 1 |
| 3 | 0011 | 3 |
| 7 | 0111 | 7 |
| 15 | 1111 | F |
| 31 | 0001 1111 | 1F |
| 63 | 0011 1111 | 3F |
| 127 | 0111 1111 | 7F |
| 255 | 1111 1111 | FF |
結局大切なのは2進数
2進数は「2」になったら桁が一つ繰り上がります。
この桁上がりする数字である「2」のことを「基数」といいます。
つまり「0」、「1」ときたら次は「2」ではなく「10」になります。
ややこしいですが、2進数に「2」は存在しません。
| 10進数 | 2進数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| ・・・ | ・・・ |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| ・・・ | ・・・ |
| 254 | 11111110 |
| 255 | 11111111 |
| 256 | 100000000 |
つまり、2進数には「0」と「1」しか存在しません。
ということはつまり数字で表現できるすべてを、
「0」、「1」で表すことができるということであり、
これはつまり概念的には、
「オフ」と「オン」で表すことができるということであり、
「×」と「〇」で表すことができるということであり、
さらに、
「No」と「Yes」で表すことができるということになります。
(この辺の概念が初学の方には重要だと思うので、まわりくどいですがあえて書きました)
コンピュータ内部の電子回路が、電流が流れている状態(オン)と流れていない状態(オフ)の2つの状態しか持たないために、この2進数の性質を利用することで、コンピュータは「0」と「1」ですべてを計算し、表現します。
2進数で小数を表す方法
2進数で小数を表すには、小数点以下の各桁に2の負のべき乗を割り当てます。
2の負のべき乗は、具体的には、小数第1位は 2-1 (0.5)、第2位は 2-2 (0.25)、第3位は 2-3 (0.125)... というように続きます。
例:0.625(10進数) を2進数で表す方法
- 0.625 は 0.5[2-1] より大きいので、2進数の小数第1位は 1 です。残りは 0.625 – 0.5 = 0.125 です。
- 0.125 は 0.25[2-2] より小さいので、2進数の小数第2位は 0 です。
- 0.125 は 0.125[2-3] と等しいので、2進数の小数第3位は 1 です。
したがって、0.625 は 2進数で 0.101 と表されます。
| 10進数 | 計算 | 2進数 |
|---|---|---|
| 0.625の小数第1位の計算→ | 0.625-0.5[2-1]=0.125 | 0.1 |
| 0.625の小数第2位の計算→ | 0.125-0.25[2-2]=-0.125 | 0.10 |
| 0.625の小数第3位の計算→ | 0.125-0.125[2-3]=0 | 0.101 |
例:0.101(2進数)を10進数で表す方法
2進小数を10進小数に変換するには、各桁の値にその桁に対応する重みを掛けて、合計します。
0.101 (2進数)
= 1[小数第1位] × 0.5[2-1 ]+ 0[小数第2位] × 0.25[2-2 ] + 1[小数第3位] × 0.125[2-3 ]
つまり、
0.101=1×0.5+0×0.25+1×0.125=
0.625(10進数)
となります。
- 10進数では有限小数であっても、2進数では無限小数になる場合があります。例えば、0.1 (10進数) は 2進数では 0.000110011… というように循環小数になります。
- コンピュータ内部では、小数は2進数で表現されますが、精度に限りがあるため、正確な値を表せない場合があります。
コンピューターで小数点を表現する方法
コンピューターで小数点を表現するときは浮動小数点数という表現方法を使います。
2進数で負の数を表す方法
まず驚きなのですが、コンピュータは足し算しかできないらしいのです。
どういうことかと言いますと、加算器という足し算の回路で計算を行っているようで、
足し算しかできないから、足し算で引き算ができるように、引き算すなわち負の数を補数で表現するのです。
要するに
補数、つまりビットを反転させて1を足した数(2の補数)を負の数として表します。
補数の考え方
- 表現したい負の数の絶対値を2進数で表します。
- その2進数の各桁の0と1を反転させます(1の補数)。
- 反転させた2進数に1を加えます。
例:-5 を2進数(8ビット)で表す
- 5の絶対値は5なので、2進数で表すと 00000101 となります。
- 各桁の0と1を反転させると 11111010 となります。
- 1を加えると 11111011 となります。
したがって、-5 は2進数(8ビット)で 11111011 と表されます。
例:8-5=3を2進数(8ビット)で表す
- 8を2進数で表す: 00001000
- -5を2進数(2の補数)で表す: 11111011
- 8の2進数と-5の2進数を足す: 00001000 + 11111011 = (1)00000011
- 桁あふれした1を無視する: 00000011 (これは10進数の3を表す)
2進数の負の数を補数で表すと…
| 10進数(正の数) | 2進数(8ビット) | 10進数(負の数) | 2の補数表現(8ビット) |
|---|---|---|---|
| 0 | 00000000 | 0 | 00000000 |
| 3 | 00000011 | -3 | 11111101 |
| 8 | 00001000 | -8 | 11111000 |
| 15 | 00001111 | -15 | 11110001 |
| 16 | 00010000 | -16 | 11110000 |
| 31 | 00011111 | -31 | 00011111 |
| 32 | 00100000 | -32 | 11100000 |
| 50 | 00110010 | -50 | 11001110 |
| 64 | 01000000 | -64 | 11000000 |
| 127 | 01111111 | -127 | 10000001 |
| 128 | 8ビットでは範囲外 | -128 | 10000000 |
2の補数のメリット
- 負の数の加算・減算が、正の数の計算と同じ回路で行えるため、コンピュータ内部での演算が効率的に行えます。
- 最上位ビット(MSB)が1であれば負の数、0であれば正の数(または0)と簡単に判別できます。
注意点
- 2の補数で表現できる負の数の範囲は、使用するビット数によって決まります。例えば、8ビットで表現できる負の数の範囲は -128 から -1 までです。
他の表現方法
2の補数の他に、負の数を表現する方法として「1の補数」や「符号ビットと絶対値」といった方法もありますが、現在では2の補数が最も一般的に利用されています。
10進数⇔2進数の変換方法
1. 繰り返し2で割る方法 (整数の場合)
- 変換したい10進数を2で割ります。
- 商と余りをメモします。
- 商が0になるまで、商を2で割る操作を繰り返します。
- 最後に得られた余りから、最初に得られた余りまでを逆順に並べると、2進数での表現になります。
例:10進数の13を2進数に変換する場合
| 割り算 | 商 | 余り |
|---|---|---|
| 13 ÷ 2 | 6 | 1 |
| 6 ÷ 2 | 3 | 0 |
| 3 ÷ 2 | 1 | 1 |
| 1 ÷ 2 | 0 | 1 |
余りを下から上に読むと、1101となります。 したがって、10進数の13は2進数では1101と表現されます。
2. 繰り返し2倍にする方法 (小数の場合)
- 変換したい10進数の小数部分を2倍します。
- 結果の整数部分をメモします。
- 整数部分を切り捨て、残った小数部分を再び2倍します。
- 小数部分が0になるか、または十分な桁数になるまで繰り返します。
- メモした整数部分を上から順に並べると、2進数での表現になります。
例:10進数の0.625を2進数に変換する場合
| 2倍 | 結果 | 整数部分 |
|---|---|---|
| 0.625 × 2 | 1.25 | 1 |
| 0.25 × 2 | 0.5 | 0 |
| 0.5 × 2 | 1.0 | 1 |
整数部分を上から読むと、101となります。 したがって、10進数の0.625は2進数では0.101と表現されます。
3.Excelで変換する
10進数⇒2進数:DEC2BIN関数 [=DEC2BIN(値,桁数)]
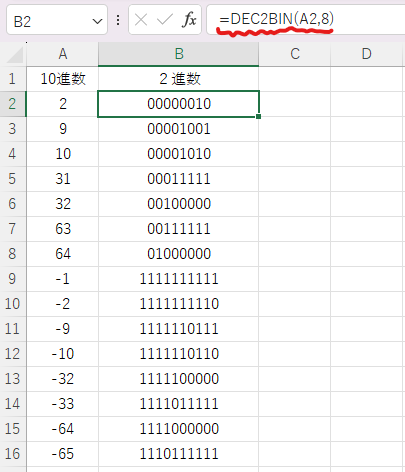
負の表現は桁数を指定しても必ず10桁の補数表現になるようです。
2進数⇒10進数:BIN2DEC関数 [=BIN2DEC(値,桁数)]
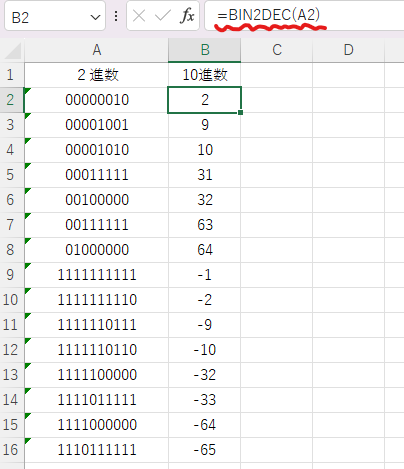
負の表現は桁数を指定しても必ず10桁の補数表現になるようです。
10進数⇒16進数:DEC2HEX関数 [=DEC2HEX(値,桁数)]
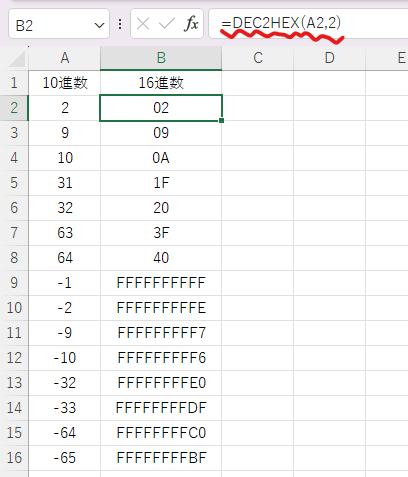
負の表現は桁数を指定しても必ず10桁の補数表現になるようです。
16進数⇒10進数:HEX2DEC関数 [=HEX2DEC(値,桁数)]
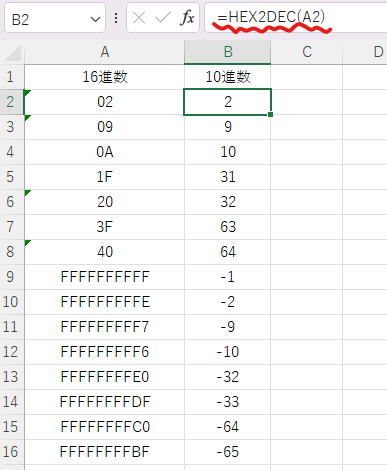
負の表現は桁数を指定しても必ず10桁の補数表現になるようです。
補足とまとめ
- 10進数の整数は、2進数では0と1の組み合わせで表現されます。
- 2進数の各桁は、右から順に2の0乗、2の1乗、2の2乗…というように、2のべき乗の重みをもちます。
- 10進数の小数も、2進数では0と1の組み合わせで表現されます。
- 2進数の小数点以下の各桁は、右から順に2の-1乗、2の-2乗、2の-3乗…というように、2の負のべき乗の重みをもちます。
- 2進数の負の数は、2の補数で表現されます。


